히스토그램에서 그릴 수 있는 직사각형 중 가장 큰 것의 넓이를 구하는 문제입니다. 제가 PS는 젬병이라 이 문제가 왜 분할 정복인지 꽤 오래 고민했습니다. 고민 끝에 반으로 쪼개서 각 부분에 대해 넓이의 최대값을 구하고 두 부분 모두 지나는 영역 중 최대 넓이를 구해서 각 최대값의 최대값을 반환하는 방식을 사용하면 될 것 같다고 생각했습니다.
이 문제는 재귀를 돌리는데, 재귀 함수는 입력으로 받은 범위를 반으로 쪼개서 앞쪽 반과 뒤쪽 반에 대해 재귀 함수를 다시 호출하여 값을 받아옵니다. 각 반쪽에 대해 값을 받으면, 두 범위를 모두 지나는 영역을 체크합니다. 두 부분을 모두 지나야 한다는 조건을 이용하여 머지 소트의 방식을 이용하여 넓이를 모두 판정할 수 있습니다. 우선 왼쪽 부분의 끝 막대와 오른쪽 부분의 첫 막대를 포함한 상태에서 넓이를 구하고, 막대의 범위를 확장해나갑니다. 확장할 때에는 각 방향에 대해 지금까지 나왔던 막대 중 가장 작은 막대의 높이를 저장합니다. 이 높이와 확장할 막대의 높이 중 작은 것을 계속 저장해가며 양쪽의 값 중 큰 값을 가지는 쪽으로 확장합니다. 확장할 때마다 범위에 속하는 모든 막대를 지나는 직사각형의 넓이를 구하고, 이 넓이 중 가장 큰 값을 구합니다. 이 값과 재귀를 통해 얻은 값들 중 가장 큰 값을 반환합니다. 아래 그림처럼 말이죠.
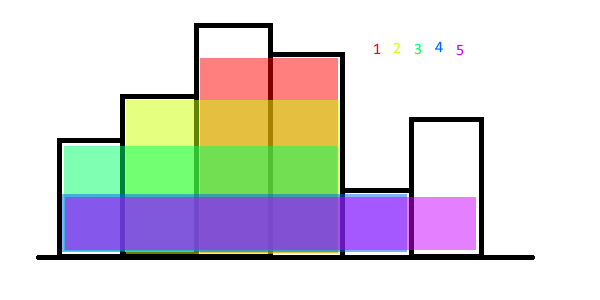
주어진 범위가 위 그림과 같을 때, 반으로 쪼갠 두 범위를 모두 지나는 넓이의 최대값은 위 그림에서 가장 큰 넓이가 됩니다. 위와 같이 정의한 재귀 함수를 전체 범위에 대해 돌린 후 나온 결과값을 출력하면 됩니다.
소스 코드
| 언어 | 코드 | 시간 |
|---|---|---|
| C++ | 코드(Github) / 코드(백준) | 2020-04-06 17:38:04 |